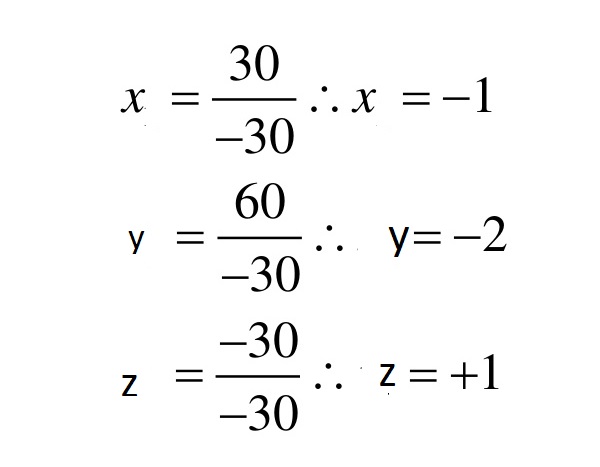Método de Cramer
Es un teorema de algebra lineal que da la solución de un sistema lineal de ecuaciones en términos de determinantes , recibe este nombre por Gabriel Kramer .
EJEMPLO :
3x – 6y + 9z = 18
2x – 4y + 5z=11
-3x -4y + 6z=17
Los coeficientes de las incógnitas se convierten en el determinante principal del sistema.
|
3 |
-6 |
9 |
|
2 |
-4 |
5 |
|
-3 |
-4 |
6 |
Ahora se multiplica, en diagonal, como se muestra a continuación.
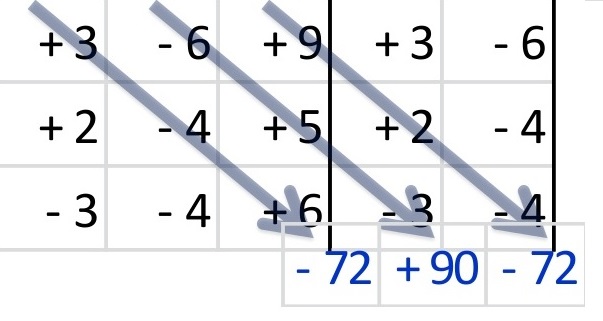
Después nuevamente se multiplica en diagonal , y se cambia el signo de los resultados.
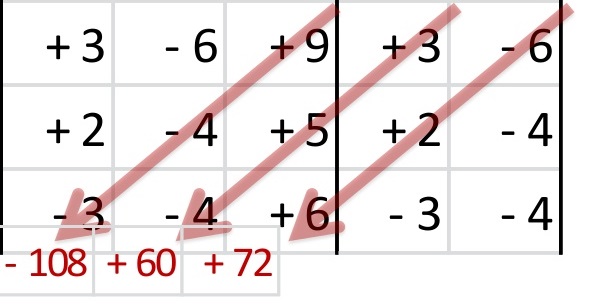
Finalmente se suman algebraicamente los seis resultados de las multiplicaciones.
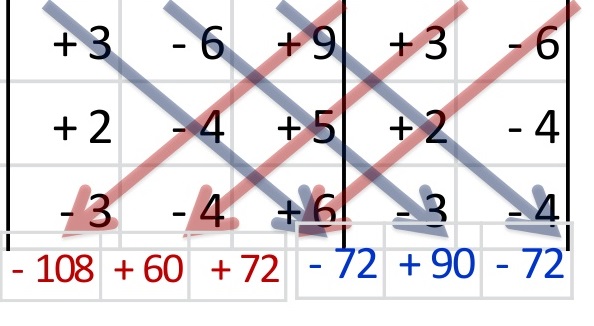
El determinante para “x” es como el determinante principal, pero se cambia la primer columna, anotando en lugar de los coeficientes, los términos independientes.
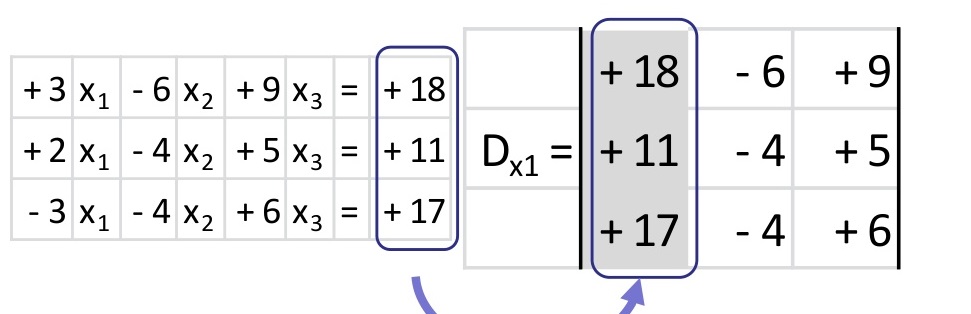
Después se multiplican las 6 diagonales (no olvides cambiar los signos en tres de ellas) y se suman los seis resultados de ellas.
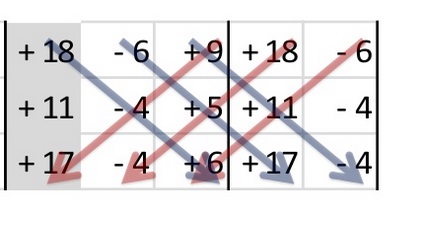
Para determinar “y” Es como el anterior solo que en esta ocasión en la segunda columna en vez de los coeficientes, se ponen los términos independientes.
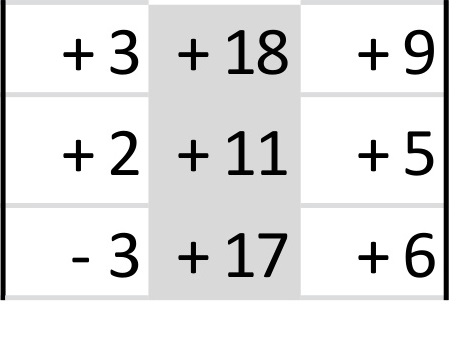
Se multiplican las 6 diagonales (no olvides cambiar los signos en tres de ellas) y se suman los seis resultados de ellas.
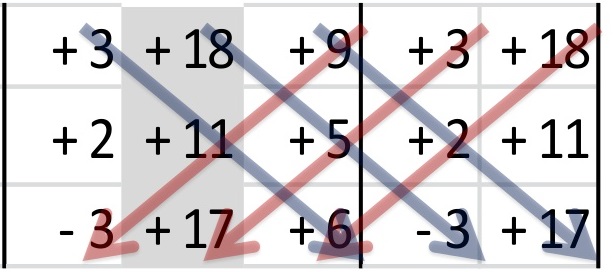
Lo mismo se hace para el determinante de z .
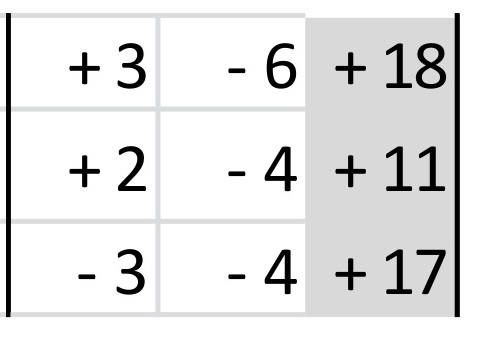
Se multiplican .
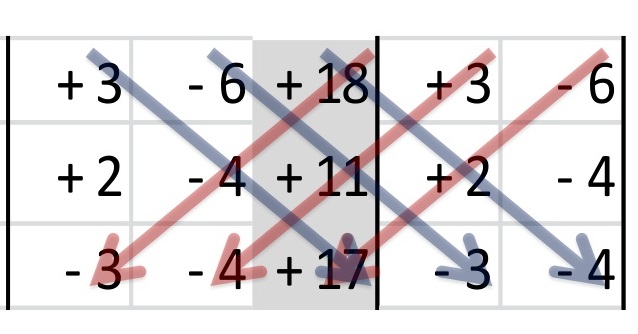
Y los determinantes finales serian:
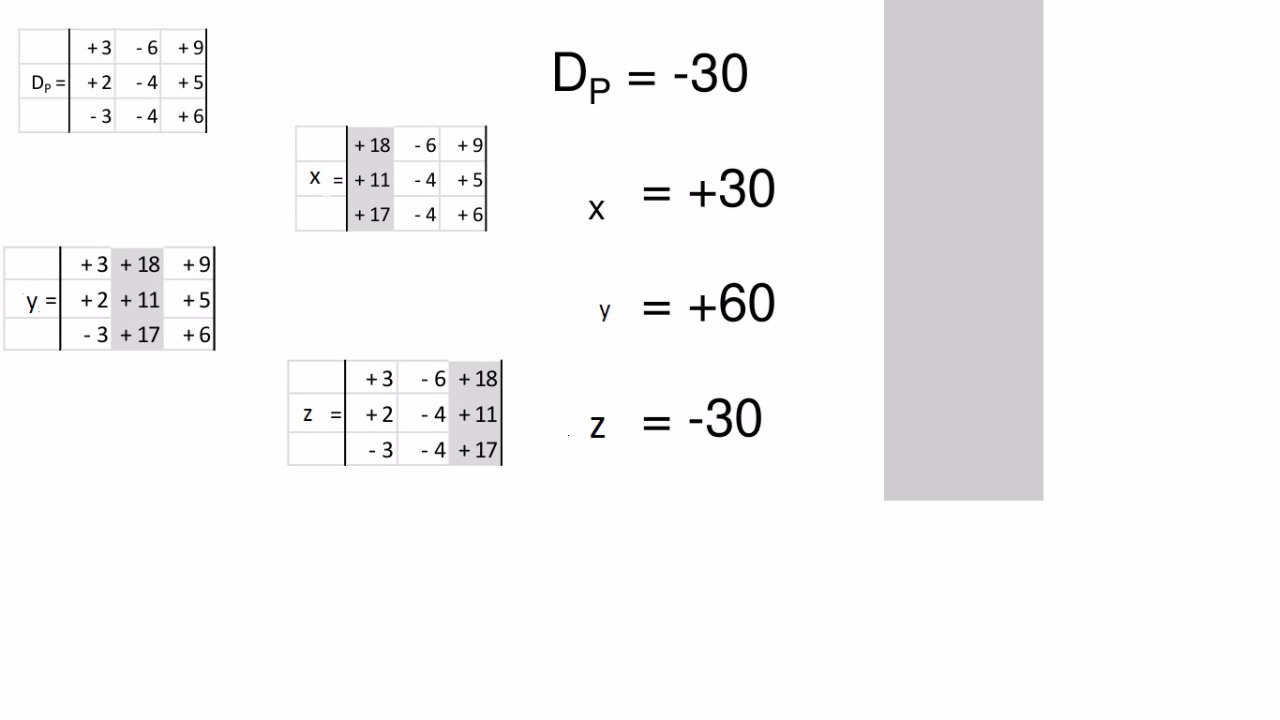
Los valores de las incógnitas se dan dividiendo los determinantes por el determinante principal.