Producto Cartesiano
El producto cartesiano de dos conjuntos es una operación, que resulta en otro conjunto, cuyos elementos son todos los pares ordenados que pueden formarse tomando el primer elemento del par ordenado del primer conjunto y el segundo elemento del par ordenado del segundo conjunto.
Existen 3 formas diferentes de representar un producto cartesiano los cuales son:
Extensión
Diagrama sagital
Gráficamente
A = {X E Z / - 4 ≤ X ≤ -3}
A = {- 4, -3}
Y
B = {blanco, verde, rojo}
Su producto cartesiano es:
A X B = {(blanco, - 4), (blanco, - 3), (verde, -4), (verde, -3), (rojo, - 4), (rojo, -3)}
Ejemplo 3:
Sean C = {a, b} y D = {1, 3, 5} Hallar: (C x D), (D x C), (C x C), (D x D). Por extensión.
C x D = {(a ,1), (a ,3), (a ,5), (b ,1), (b ,3), (b ,5)}
D x C = {(1, a), (1, b), (3, a), (3, b), (5, a), (5, b)}
C x C = {(a, a), (a, b), (b, a), (b, b)}
D x D = {(1, 1), (1, 3), (1, 5), (3, 1), (3, 3), (3, 5), (5, 1), (5, 3), (5, 5)}
Ejemplo 4:
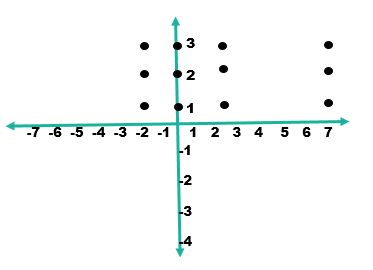
Sea A = {- 2, 0, 3, 7} y B = {1, 2, ,3} obtener el producto cartesiano A x B y B x A y dibujar su gráfica.
A x B = {(-2, 1), (-2, 2), (-2, 3), (0, 1), (0, 2), (0, 3), (3, 1), (3, 2), (3, 3), (7, 1), (7, 2), (7, 3)}
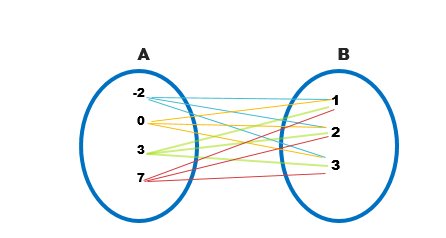
B x A = {(1, -2), (1, 0), (1, 3), (1, 7), (2, -2), (2, 0), (2, 3), (2, 7), (3, -2), (3, 0), (3, 3), (3, 7)}
Diagrama sagital:
Plano cartesiano: